python 数据结构

Hash Table (Dictionary Implementation in Python)

Posted by Annie's Blog on June 5, 2016

Python中字典的内部实现是Hash Table

建立Hash Table

字典实际上是一个hash table，而hash table实际上是一个数组

Hash Table实际上是一个数组，数组中存放着键值对(Key Value Pairs)，数组的下标则是由键(Key)通过hash函数算出来的一个整数

一个空字典是一个长度为8的数组(这个数组拥有连续的内存地址)

将键(Key)映射成数组下标(Index)通常经过两步

  • Step 1 预哈希(Prehash)得到哈希码(hashcode):

    先将键(Key)映射成非负整数

    在Python中，hash(x)即是对x的prehash,如：

    hash(‘a’) = 12416037344

    12416037344就是’a’的hashcode

    相同的键对应的hashcode相同

  • Step 2 哈希(Hash)得到数组下标(index):

    将第一步prehash得到的hashcode进一步映射成数组下标

    数组下标是［0，N-1］中的一个整数 (其中N是数组长度)

字典中用如下方法映射键与数组下标

假设现在用一个大小为x的数组来存放键值对，则键(key)与数组下标(index)的映射关系为：

index = hash(key) & mask

(mask = x-1

 x is the size of the array)

字典的key只能是不可变(immutable)对象，不能是可变(mutable)对象，因为如果key变了，其hashcode也会变，算出的数组下标也会变，从而会导致在查找时无法找到对应的value。

字典是无序的

  • 由于字典实际上是存储在一个hash table中的，因此，输出字典中各元素时，其顺序并不会按照元素输入的顺序，而是按照在hash table中存放的顺序。 例如：
>>> d = {}

>>> d['ftp'] = 21
>>> d['ssh'] = 22
>>> d['smtp'] = 25
>>> d['www'] = 80
>>> d['time'] = 37

此时，字典d对应的hash table如下：

image

>>> print d
{'ftp': 21, 'www': 80, 'smtp': 25, 'ssh': 22, 'time': 37}
  • 即使是两个元素完全一样的字典，由于其各个元素插入顺序额不同，其键的顺序也会不同。假设现有两个所包含元素完全相同的字典，但各元素插入顺序不同：
>>> a = {'smtp': 21, 'dict': 2628', 'svn': 3690, 'ircd': 6667, 'zope': 9673}

>>> b = {'ircd': 6667, 'zope': 9673, 'smpt':21, 'dict': 2628, 'svn': 3690}

字典a, b对应的hash table如下图：

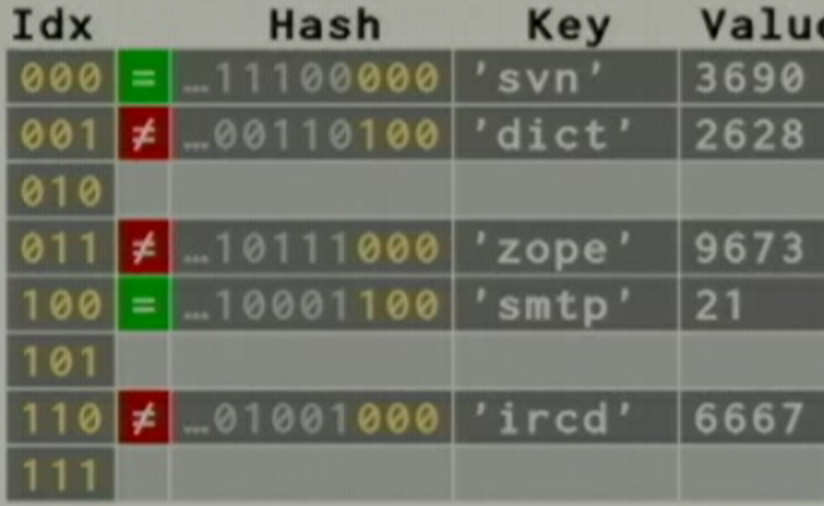
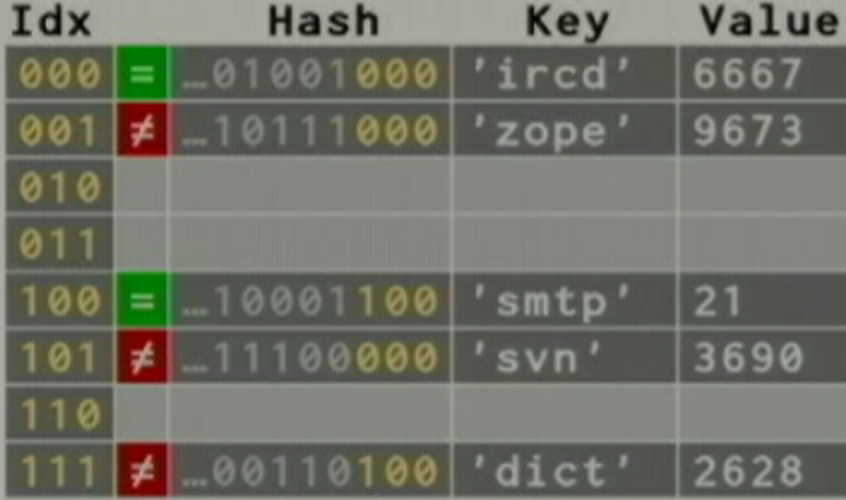
image image

字典a, b的key的输出顺序如下：

>>> a.keys()
['svn', 'dict', 'zope', 'smpt', 'ircd']
>>> b.keys()
['ircd', 'zope', 'smpt', 'svn', 'dict']
  • 插入操作可能会使字典重排序，因此在迭代时不允许向字典插入元素。 例如：
>>> d={'a':1,'b':2,'c':3}
>>> for key in d:
>>>  	d['d'] = 4
RuntimeError: dictionary changed size during iteration

解决冲突

冲突

在将键映射成数组下标时，通常会出现冲突，例如：

数组长度是8

hash(‘a’) & 7 = 0 －－ ‘a’存储在下标0中

hash(‘b’) & 7 = 3 －－ ‘b’存储在下标3中

hash(‘c’) & 7 = 2 －－ ‘c’存储在下标2中

hash(‘z’) & 7 = 3 －－ ‘z’存储在下标3中，与’b’发生冲突

解决冲突的方法

  • 通常有2种解决冲突的方法：

    • 链表法(Seperate Chaining)： 当两个键映射的下标冲突时，可用一个链表将这些冲突的键值对存储在同一个下标下，这就是链表的解决办法。 但是链表法有可能破坏时间复杂度，使之不能维持在 O(1)。通常认为，当n / N > 0.75（n为键值对数目，N为数组长度） 时，应增大数组长度以使时间复杂度保持在O(1)。

    • 开放定址法(Open Addressing)： 在开放定址的解决办法中，如果有冲突发生，那么就要尝试选择另外的单元，直到找到空的单元为止。

  • 在字典的实现中，用到了开放定址法(Open Addressing)来解决冲突

    冲突会导致键值对并不一定存放在其对应的下标中

Resizing

  • 为了尽量避免冲突的出现，字典在填满数组总长度的2/3时就会进行数组大小的调整(resize)：
    • 当键值对总数 < 50k时，size x 4
    • 当键值对综述 > 50k时，size x 2

    当然，在把旧hash table中的内容搬移到新hash table中时，由hashcode计算数组下标的策略也要有所改变

  • 由于字典总是在2 / 3满时就进行resize以避免冲突，可见字典的战略是用空间换时间，如果想节省空间，可以选择用元组。

查找操作

  • 当查找某个键所对应的值时，先重复一遍插入时的操作（prehash得到hashcode, hash得到数组下标index），再查看该下标中存储的键是否是要查找的键，若不是，则继续查看下一个可能冲突的下标，直到找到匹配的键－返回其对应的值 或 找到一个空的下标－报错。

  • 并不是所有查找操作都耗费相同的时间。有些查找或许在第一个下标处就找到了匹配的值，有些查找则需经历好几个下标才找到匹配的值。

删除操作

  • 当删除键值对时，并不能直接删去，而应将其键标记为dummy。

  • 如果直接删去，将会导致与该键冲突的其他键无法被找到，因为在查找操作中，只要遇到了空的下标，将会报错而不会往下继续查找，而如果遇到了标记为dummy的键，将会继续往下查找。