可以用动态规划求解的问题的特点
最优化问题
-
最优子结构性质:当问题的最优解包含了其子问题的最优解时,成该问题具有最优子结构性质
-
重叠子问题:每次产生的子问题并不总是新问题,有些子问题被反复计算多次
满足以上两个特点的问题可考虑用动态规划求解
例子1 背包问题
问题
给定n种物品和一背包,物品i的重量是Wi,其价值为Vi,背包的容量为C。问应如何选择装入背包的物品(物品不能分割),使得装入背包中物品的总价值最大?
问题抽象化
用Xi表示是否把物品i放入背包中 Xi = 1 表示把物品i放进背包中 Xi = 0 表示不把物品i放进背包中
我们要求的是
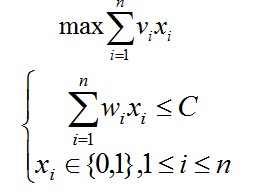
问题分析
用m[i, j]表示 在物品i, i+1, i+2, …, n中选择放入到背包中的物品时价值最大的组合
j表示背包此时的容量
m[0][C]就是我们要求的值
可得推导公式如下:
m[i][C'] = max{ m[i+1][C'], m[i+1][C'-w[i]]+v[i] }
即最优化结果为:
‘不放入第i种物品:剩下不考虑第i种物品时的最优化结果’ 和 ‘放入第i种物品:第i种物品的价值+剩下不考虑第i种物品时的最优化结果’ 中的较大值
假设:
n=3,c=6,w={4,3,2} v={5,2,1}
则 我们要求的是m[0][6]
边界条件:
当i>=3时,m=0
当j<=0时,m=0
推导过程如下
m[0][6] = max{ m[1][6], m[1][6-w[0]]+v[0] }
= max{ m[1][6], m[1][2]+v[0] }
= 6
m[1][6] = max{ m[2][6], m[2][6-w[1]]+v[1] }
= max{ m[2][6], m[2][3]+v[1] }
=3
m[2][6] = max{ m[3][6], m[3][6-w[2]+v[2]] }
= max{ m[3][6], m[3][4]+v[2] }
= 1
m[2][3] = max{ m[3][3], m[3][3-w[2]]+v[2] }
= max{ m[3][3], m[3][1]+v[2] }
=1
m[1][2] = max{ m[2][2], m[2][2-w[1]]+v[1] }
= max{ m[2][2], m[2][-1]+v[1] }
= 1
m[2][2] = max{ m[3][2], m[3][2-w[2]]+v[2] }
= max{ m[3][2], m[3][0]+v[2] }
= 1
例子2 奖券兑换问题
背包问题的一个变形
问题
小Ho现在手上有C张奖券,而奖品区有N件奖品,分别标号为1到N,其中第i件奖品需要w(i)张奖券进行兑换,同时也只能兑换一次,为了使得辛苦得到的奖券不白白浪费,小Ho给每件奖品都评了分,其中第i件奖品的评分值为v(i),表示他对这件奖品的喜好值。现在他想知道,凭借他手上的这些奖券,可以换到哪些奖品,使得这些奖品的喜好值之和能够最大。
问题抽象化
用Xi表示是否兑换第i种奖品
Xi = 1表示兑换
Xi = 0表示不兑换
我们要求的是
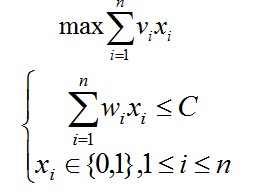
问题分析
用opt[i, C']表示用C’张奖券换i, i+1, …, n-1种奖品时评分的最大值
C’表示所需奖券C’张
opt[0, C]就是我们要求的值
可得推导公式如下:
opt[i][C'] = max{ opt[i+1][C'], opt[i+1][C'-w[i]]+v[i] }
即最优化结果为:
‘不兑换第i种物品:剩下不考虑第i种物品时的最优化结果’ 和 ‘兑换第i种物品:第i种物品的价值+剩下不考虑第i种物品时的最优化结果’ 中的较大值
代码实现
w = [144, 487, 210, 567, 1056]
v = [990, 436, 673, 58, 897]
opt = {}
def cal(n, c):
if n >= ngifts or c <= 0:
return 0
if opt.get((c, n)):
return opt[(c, n)]
else:
ret = -1
for k in range(2):
temp = cal(c - k*w[n], n+1)
if c - k*w[n] >= 0:
temp += v[n]*k
if temp > ret:
ret = temp
opt[(n, c)] = ret
return ret
print cal(0, 1000)
例子3 饮料供货问题
背包问题的一个复杂版本
编程之美P43